Order Statistics

 

B.Sc. III    Semester- VI    Statistics –XIII

Probability Theory and Applications

Unit 1:  Order Statistics and Convergence

1.1   Order Statistics

        Let X1, X2, X3, …..,Xn  be a random sample of size n from a continuous distribution with p. d. f. f(x) and c .d. f. F(x).

         Let,   X(1) = min { X1, X2, X3, ….., Xn }

                  X(2) = 2nd min { X1, X2, X3, ….., Xn }

                  X(3) = 3rd min { X1, X2, X3, ….., Xn }

                  …..

                 X(n) = nth min { X1, X2, X3, ….., Xn } =  max{ X1, X2, X3, ….., Xn }

then X(1) , X(2) , ……, X(n) are  known as the order statistics corresponding to the random sample X1, X2, X3, …..,Xn. For convenience, we denote   Y1 = X(1) , Y2 = X(2) , Y3 = X(3) ,….., Yn = X(n) . Thus Y1, Y2, Y3,…..,Yn  are the order statistics corresponding to the random sample X1, X2, X3, ….., Xn.

Note that        X(1) < X(2) <……< X(n)        i.e.     Y1< Y2< Y3,…..<Yn .

Note: Let X1, X2, X3, X4, X5 be i. i. d.  random variables with a distribution F with a range of              (a, b). We   can relabel these X’s such that their labels correspond to arranging them in                 increasing order so that   X(1) ≤ X(2) ≤ X(3) ≤ X(4) ≤ X(5) .

                                   X(1)       X(2)        X(3)        X(4)        X(5)

                         

                           a       X5        X1          X4          X2          X3      b

                 In the case where the distribution F is continuous we can make the stronger statement that X(1) < X(2) < X(3) < X(4) < X(5) Since P(Xi = Xj) = 0 for all i ≠ j for continuous random variables.

Distribution of 1st order statistics Y1   i.e. X(1)  or Xmin 

        Let X1, X2, X3, …..,Xn  be a random sample of size n from a continuous distribution with p. d. f. f(x) and c .d. f. F(x). Let Y1 =  min { X1, X2, X3, ….., Xn } i.e. Y1 is first order statistics corresponding to the random sample X1, X2, X3, …..,Xn.

Let g1(y) be the p. d. f. and G1(y) is a c. d. f. of Y1.

By defn of  c. d. f., we have

                                         G1(y) = P [Y1 ≤ y] = P [min {X1, X2, X3, ….., Xn } ≤ y ]

                                                                         = 1- P [min {X1, X2, X3, ….., Xn } ＞ y ]

                                                                         = 1 - P [each of Xi’s ＞ y ]

                                                                         = 1- P [X1 ＞  y, X2 ＞  y, …,  Xn ＞ y]

                                                                         = 1- P [X1＞ y] . P[ X2 ＞y]…… P[ Xn ＞y].

                                                                         = 1-  ∏  P [Xk ＞ y]

                                                                         = 1- ∏  [1- P (Xk ≤  y)]

                                                               G1(y) = 1-∏ [1- F (y)]                                                                                                                ∴   G1(y) = 1- [1- F (y)]n

         p. d. f. of first order statistics Y1 is ,

                                                                     g1(y) =d/dy  G1(y) =  {1- [1- F (y)]n}

                                         = 0 – n  [1- F (y)]n-1 [-f(y)]

                                                                  g1(y) = n [1- F (y)]n-1 [f(y)]

Ex: Let X1, X2, X3, …..,Xn  be a random sample from U(0,1). Obtain p. d. f. of first order statistics X(1)   and  hence find E(X(1) ) .

Soln : Here X has   uniform distribution  i.e. X  ̴  U (0,1) , the p. d. f. of X is given by

                     f(x) = 1,        0 ≤ X ≤ 1

                            = 0,        otherwise

      Here X1, X2, X3, …..,Xn  is a random sample from U(0,1).

      Let, Y1 = X(1)   = min { X1, X2, X3, ….., Xn }.

      We have c. d. f. of X is, F(x) = P[X ≤ x] = ∫ f(t) dt = ∫ 1 dt =[t] (0 to x)  = x ;  0 ≤ x ≤ 1.

   p. d. f. of first order statistics Y1 is,

                                                                 g1(y) = n [1- F (y)]n-1 [f(y)]

                                                                           = n [1- y1]n-1 . 1

                                                         g1(y) = n [1- y1]n-1          0 ≤ y1≤ 1

                                                                     = 0,        otherwise

This is p. d. f. of beta distribution of first kind with parameters (1,n).

i. e.  Y1 ̴ β1 ( 1,n).

Now,

            E [X(1)] =  E [Y1] =  ∫ y1 g1(y) dy =  ∫  y1 n [1- y1]n-1 dy1  =  n ∫ y1 [1- y1]n-1 dy1 

                         = n  ∫  (y1)2-1 [1- y1]n-1 dy1 

                         = n β1 (2, n) =  1/n+1

 ***

Distribution of nth order statistics Yn   i.e. X(n)  or X max 

               Let X1, X2, X3, …..,Xn  be a random sample of size n from a continuous distribution with p. d. f. f(x) and c .d. f. F(x). Y1, Y2, Y3,…..,Yn  are the order statistics corresponding to the random sample X1, X2, X3, ….., Xn. Here Yn =  max { X1, X2, X3, ….., Xn } = X max .

Let gn (y) be the p. d. f. and Gn(y) is a  c. d. f. of Yn.

By defn of c. d. f., we have

                                         Gn(y) = P [Yn ≤  y] = P [max {X1, X2, X3, ….., Xn } ≤  y ]

                                                                         =  P [each of Xi’ s  ≤  y ]

                                                                         = P [X1 ≤  y,  X2 ≤  y,…… ,Xn ≤  y].

                                                                         =  P [X1 ≤  y] . P[ X2 ≤  y]…… P[ Xn ≤  y].

                                                                        = ∏  P [Xk ≤  y]

                                                                         =  ∏ F (y)

                                                              Gn(y) =  [ F (y)]n

       ∴     p. d. f  of  n th  order statistics Yn is ,

                                                           gn(y) =d/dy  Gn(y) = d/dy [ F (y)]n

                                      ∴   gn(y) =  n  [ F (y)]n-1 [f(y)]

                                                                               ***

Ex: Let X1, X2, X3, …..,Xn  be a random sample from U(0,1). Obtain p. d. f. of maximum( nth order statistics X(n) ) .

Soln : Here X has   uniform distribution  i.e. X  ̴  U (0,1) , the p. d. f. of X is given by

                     f(x) = 1,        0 ≤ X ≤ 1

                            = 0,        otherwise

      Here X1, X2, X3, …..,Xn  is a random sample from U(0,1).

      Let, Yn = X(n)   = max { X1, X2, X3, ….., Xn }.

      We have c. d. f. of X is, F(x) = P[X ≤ x] = ∫ f(t) dt = ∫ 1 dt = [t] (0 to x) = x ;  0 ≤ x ≤ 1.

   p.d.f. of nth  order statistics Yn is,

                                                                 Gn(y) = n [ F (y)]n-1 [f(y)]

                                                                           = n [ yn]n-1 . 1

                                                         gn(y) = n  ynn-1          0 ≤ yn ≤ 1

                                                                     = 0,        otherwise

This is p.d.f. of beta distribution of first kind with parameters (n,1).

i. e.  Yn ̴  β1 (n,1).

 

Note: If X1, X2, X3, …..,Xn  be a random sample from U(0,1), then

        i) Y1 =  min { X1, X2, X3, ….., Xn } ̴ β1 ( 1,n).

       ii) Yn =  max { X1, X2, X3, ….., Xn } ̴ β1 ( n,1).


***



***

***

J  Joint p. d. f. of ith and jth order statistics:


CC Consider, 


***



***



***
Distribution of range :

***






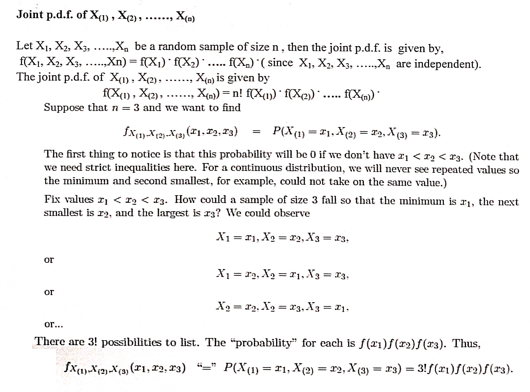
Comments

Post a Comment

Popular posts from this blog

B. Sc. Part I Semester I I.I Introduction to Statistics :Nature of Data, Sampling, Classification and Tabulation

Image
  B. Sc. Part 1 Semester 1 DSC-7A-STATISTICS-1 (DESCRIPTIVE STATISTICS-1) Theory: 30 hrs. Mark 50 (Credits: 02)              ‘Statistical thinking will one day be necessary for effective             Citizenship as the ability to read and write’ - H.G. Wells   1.1 Introduction to Statistics: Meaning of the word Statistics Statistics is as old as language Statistics is in use from the time when man began to count & measure: The word ‘Statistics’ has several meanings.  Statistics-Plural- Figures, Numbers, Data (for ex. statistics of a batsman)                 Singular Methods, Science, Subject itself In ancient days kings used to maintain records of manpower, wealth, population, income, taxes & military etc. The word 'Statistics seems to be derived from the Italian word 'statista', G...
Read more
Image
  B. Sc. III Semester V Subject-Statistics-XI DSE-E15: Sampling Theory Theory: 36 Hours. (Credit 02)   Unit-1     Simple and Stratified Random Sampling: Introduction:         Sampling is quite often used in our day to day practical life. For example -   in a shop we assess the quality of sugar, wheat or any   other commodity by taking a handful of it from the bag and then decide to purchase it or not. A housewife normally tests, the cooked products to find if they are properly cooked and contain the proper quantity of salt. In sampling theory we first define the following terms. i)   Population (Universe) The group of individuals under study is called population or universe.   (The totality of the objects of study)   For example -if we are going to study the economic conditions of primary teachers in Maharashtra state, then the total of all the primary teachers in Maharashtra state is...
Read more
Image
  RELIABILITY THEORY INTRODUCTION:  ©                In day-to-day life we come across several types of machines, equipment, systems such as radio set, T. V. set, vehicle, electric bulb, computer, music system etc. We always ask questions to manufacture that how long the machine will work without any trouble. What is the guarantee period of the item? Answers to such questions are based on the life time of the components of machine as well as the entire assembly. A reliability theory deals with extensive study of life time of components and machines. This is one of the important branch having wide applications in the manufacturing process.                    Reliability theory is concerned with determining a probability that, a system of several components is functioning i.e. working at a specified time ‘t’. The se...
Read more