RELIABILITY
THEORY
INTRODUCTION:
In day-to-day life we come
across several types of machines, equipment, systems such as radio set, T. V.
set, vehicle, electric bulb, computer, music system etc. We always ask questions
to manufacture that how long the machine will work without any trouble. What is
the guarantee period of the item? Answers to such questions are based on the
life time of the components of machine as well as the entire assembly. A
reliability theory deals with extensive study of life time of components and
machines. This is one of the important branch having wide applications in the
manufacturing process.
Reliability theory is
concerned with determining a probability that, a system of several components
is functioning i.e. working at a specified time ‘t’. The several components of
a system may be arranged in a series system or a parallel system or mixed.
Series system of components will function if all of its components are
functioning; while a parallel system will function if at least one of its
components is functioning. For
example; i) switch, holder and electric bulb are connected or arranged in
series system. ii) Amplifier and speaker in a sound system are connected in series
system. This system fail if any one of its components fails i.e. sound system
is working if both amplifier and speaker are functioning or working. iii)
Speakers in sound system are arranged in parallel system. If at least one
speaker is working then system is working.
iv) Breaks of a bike are
connected in parallel system.
System: A system is a technical configuration of two
or more components (or items or units or parts) which is designed to perform
one or more functions.
Structure Function:
Consider a system of ‘n’ components and
suppose that each component is either working i.e. functioning or not working
i.e. fails. To indicate whether or not the ith component is
functioning we define indicator variable Xi; i = 1, 2, ……, n as below.
Xi = 1; if ith
component is functioning
= 0; if
ith component is not functioning.
Then vector X = (X1, X2,
Xi, ,………., Xn) is called state vector of a system at time
‘t’. It indicates which of the components are functioning and which are in
failure state.
For
example; i) X = (1, 1, 1, 1) indicates that all four components of a
system are functioning. ii) X =
(1, 0, 0) indicates that first component of a system is
functioning and second and third components have failed.
iii) Series system:
X = (1, 1) is state vector of series system of two components which is
functioning, since series system is working if both the components are working.
If X = (1, 0) or
(0, 1) or (0, 0) then system fails.
iv) Parallel system:
If two components of a system are connecting in parallel then this system is
working if state vector is, X = (1, 0) or (0, 1) or (1, 1) i. e.
parallel system of two components is working if at least one of component is
functioning.
Definition of Structure Function:
Reliability Block Diagram:
The physical configuration of
components assembled in a system is often used to model system reliability. Reliability
block diagram is a diagrammatic representation of components in the system
which is used to model system reliability. The rectangular blocks or boxes
represent the components of the system and either component numbers or
reliabilities are placed inside the boxes. With the help of this diagram we can
answer the questions like – which combinations of the components must function
for the system to function and which ones can fail without affecting it? A
reliability block diagram is often helpful in visualizing the way components
are arranged.
Types of systems
i) Series System of n
Components (Series Structure):
A series system
functions if all of its components are working. The reliability block diagram
of series system of n components is as below
Examples:
1.
A calculator is a series system of four components viz. keyboard, display, microprocessor and battery. Since, failure
of any component results in system failure.
2.
Amplifier and speaker in sound system
are connected in series.
3.
The wheels of two wheeler are in series.
4.
The starter and choke of tube light are
in series.
5.
Pairs of shoes are also an example of a
series system.
ii) Parallel System of n Components (Parallel
Structure):
A parallel system functions
if at least one of its components are working or functioning. The reliability
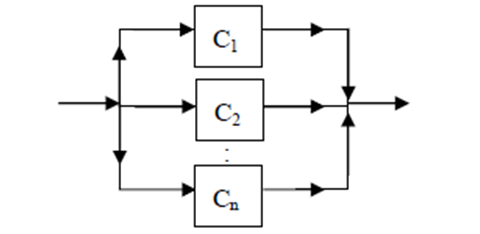
block diagram of parallel system of n components is as below.
Examples:
1.
The brakes of automobile are in parallel.
2.
Speakers of a sound system are in parallel.
3.
The eyes of human being are in parallel (since we can see when any one eye is
good).
4.
The ears of human being are in parallel.
5.
The kidneys are in parallel.
iii)
The 2 out of 3 system:
![]()
iv) k out of n system (k ≤ n):
It is a system of n components such that system is functioning iff at least ‘k’ out of ‘n’ components are
functioning. If X = (X1, X2, ….., Xi, ………., Xn)
is state vector of a system then its structure function is given by,
Note that, series system and parallel system are
special cases of ‘k’ out of ‘n’ system. The series system is ‘n’ out of ‘n’
system where as parallel system is ‘1’ out of ‘n’ system.
Examples:
1.
Bicycle wheel needs only k spokes out of n to function hence it is a k out of n
system.
2.
A four cylinder car engine can function if any three cylinders are working;
hence it is a 3 out of 4 system.
3.
Human jaws has 32 teeth, if some of teeth are lost one can chew the food, hence
it can be viewed as k out of 32 system.
Example: Write structure
function of following system.
Solution:
The above system is functioning iff component ‘1’ and at least one out of ‘2’
and ‘3’ functioning. If X = (x1, x2, x3)
is state vector of a system then its structure function is given by considering
the parallel assembly of C2 and C3 as a single component
denoting it by A. Thus the system can be viewed as a series assembly of two
components C1 and A.
Since A is parallel assembly of C2
and C3 , the structure
function
XA = Max { X2, X3} = 1- (1- X2 ) (1- X3 ) = X1 × { X2
+ X3- X2 X3}
=
X1X2 + X1X3 - X1X2X3 where Xi = 0,1 for i= 1,2,3
The above system can be
equivalently represented as;
Ex.: Draw a block diagram and obtain structure function of a 2 out of 3 system.
Sol.: 2
out of 3 system functions, if at least 2 components work. If components (1, 2)
= A or (1,3) = B or (2,3) = C work,
system works. Thus, these pairs are to be connected in parallel and the
components in every pair are required to be in series. The reliability block
diagram is,
= X1X2+ X1X3 +X2X3 - X12X2X3 -X1X22X3 -X1X2X32 + X12X22X32

B.Sc. (Part-III) (Semester- VI) Internal Examination, Feb 2024
STATISTICS
Probability Theory and Applications
(Paper-XIII)
Sub. Code: 81692
Day and Date:
Total marks: 40
Time:
Instructions: 1) All questions are compulsory.
2) Figures to
the right in the bracket indicate full marks.
Q 1) Choose the most correct alternative: (08)
c) Both (a) and (b) d) None of
these
2. If Xn converges to x in probability, then……..
a) Xn 2 converges to x in probability b) Xn 2 converges to x 2 in probability
c) Xn 2 converges to x in
quadratic mean d) Xn 2
converges to x 2
3. Which of the following is order Statistics?
a)
Range b) Mean c) Median d) Mode
a) 0 and 1 b) -1 and 1 c) 0 and ∞
d) -∞ and∞
a)‘n’ b) 1
c) 2n
d) n C k
7.
The reliability of parallel system of n components is.............
a) p n-1 b) 1- (1-p) n c) 1- (1-p) n-1 d) pn
8. For a
series system of two components having 0.5 reliability each the reliability of
a system is........
a) 0.25 b) 0.75 c) 0.5 d) 1
Q 2) Attempt any two of
the following: (16)
a) State and prove the weal law of large numbers (WLLN) for i. i. d. random variables.
c) If T is a lifetime of a component having exponential distribution with parameter ϴ , then find the i) Distribution function ii) Survival function iii) Hazard rate function of T and verify that E(T) = ꭍ R(t) dt (range 0 to ∞)
P [| X- µ| > 1.5ơ]































































Comments
Post a Comment